s números inteiros são os números positivos e negativos, que não apresentam parte decimal e, o zero. Estes números formam o conjunto dos números inteiros, indicado por ℤ.

Não pertencem aos números inteiros: as frações, números decimais, os números irracionais e os complexos.

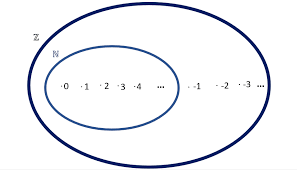
O conjunto dos números inteiros é infinito e pode ser representado da seguinte maneira:

ℤ = {…, – 3, – 2, – 1, 0, 1, 2, 3,…}

Os números inteiros negativos são sempre acompanhados pelo sinal (-), enquanto os números inteiros positivos podem vir ou não acompanhados de sinal (+).

O zero é um número neutro, ou seja, não é um número nem positivo e nem negativo.

A relação de inclusão no conjunto dos inteiros envolve o conjunto dos números naturais (ℕ).

Todo número inteiro possui um antecessor e um sucessor. Por exemplo, o antecessor de -3 é -4, já o seu sucessor é o -2.

Representação na Reta Numérica

Os números inteiros podem ser representados por pontos na reta numérica. Nesta representação, a distância entre dois números consecutivos é sempre a mesma.

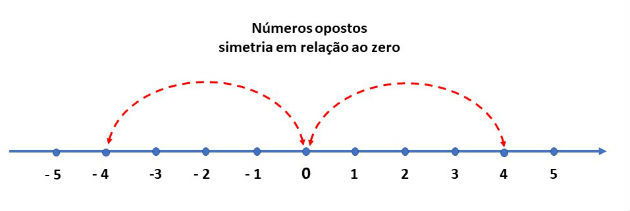
Os números que estão a uma mesma distância do zero, são chamados de opostos ou simétricos.

Por exemplo, o -4 é o simétrico de 4, pois estão a uma mesma distância do zero, conforme assinalado na figura abaixo:

Subconjuntos de ℤ

O conjunto dos números naturais (ℕ) é um subconjunto de ℤ, pois está contido no conjunto dos números inteiros. Assim:

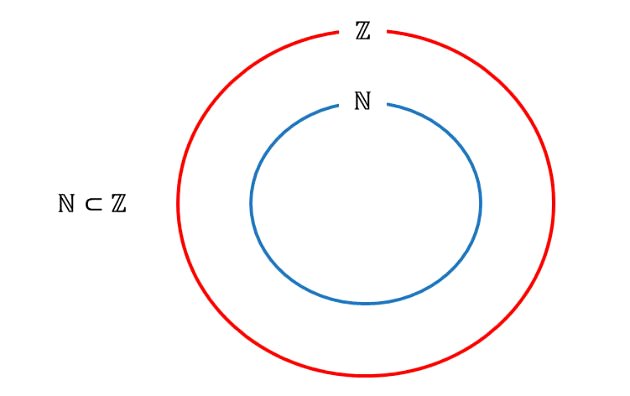
Além do conjunto dos números naturais, destacamos os seguintes subconjuntos de ℤ:

• ℤ* : é o subconjunto dos números inteiros, com exceção do zero. ℤ* = {…, -3,-2,-1, 1, 2, 3, 4, …}
• ℤ₊ : são os números inteiros não-negativos, ou seja ℤ₊ = {0, 1, 2, 3, 4, …}
• ℤ _ : é o subconjunto dos números inteiros não-positivos, ou seja ℤ_= {…, -4,-3,-2,-1, 0}
• ℤ*₊ : é o subconjunto dos números inteiros, com exceção dos negativos e do zero. ℤ*₊ = {1,2,3,4, 5…}
• ℤ*_{_} : são os números inteiros, com exceção dos positivos e do zero, ou seja ℤ*_= {…, -4,-3,-2,-1}