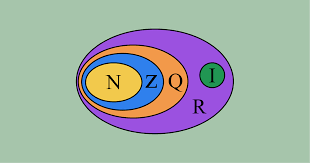
Os números com características semelhantes foram são agrupados em conjuntos numéricos. São eles:
- Números naturais (N)
- Números inteiros (Z)
- Números racionais (Q)
- Números irracionais (I)
- Números reais (R)
Números naturais (N)

Trata-se de um conjunto infinito de números, que são inteiros e positivos, utilizados na contagem.
O conjunto dos números naturais é representado por:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … }
Os números que fazem parte desse conjunto são utilizados para contar e ordenar. Os números naturais podem ser obtidos adicionando uma unidade ao número anterior da sequência.
Números inteiros (Z)
Esse conjunto infinito abrange os números que são positivos e negativos. Sendo assim, ele reúne os números naturais e seus opostos.
O conjunto dos números inteiros é representado por:
ℤ = {…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, …}
Na representação dos elementos do conjunto, os inteiros negativos são escritos com o sinal (–) e os inteiros positivos apresentam o sinal (+). Esses números são utilizados, por exemplo, para indicar grandezas, como a temperatura.
Números racionais (Q)
Esse conjunto apresenta os números que podem ser escritos na forma de fração. Sendo , com b ≠ 0, temos os seguintes elementos desse conjunto:
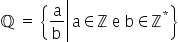
Observe que, todos os números são inteiros, mas b representa os inteiros não nulos. Portanto, Z é um subconjunto de Q.
São exemplos de números racionais: 0, ± 1, ± 1/2, ± 1/3, ±2, ± 2/3, ± 2/5, ± 3, ± 3/2, etc.
Os números racionais podem ser números inteiros, decimais exatos ou dízimas periódicas.
Números irracionais (I)
O conjunto dos números irracionais reúne os números decimais infinitos e não periódicos. Portanto, esses números não podem ser representados por frações irredutíveis.
Alguns exemplos de números irracionais:
- √2 = 1,414213562373…
- √3 = 1,732050807568…
- √5 = 2,236067977499…
- √7 = 2,645751311064…
Números reais (R)
Os números reais correspondem a união dos conjuntos de números: naturais (N), inteiros (Z), racionais (Q) e irracionais (I).
O conjunto dos números reais pode ser representado da seguinte forma: R = Q U (R – Q), pois se um número real é racional ele não pode ser também irracional e vice-versa.